一种多模态电力系统的异步控制方法、设备及存储介质-j9九游会真人

1.本发明涉及电力自动化技术领域，具体为一种多模态电力系统的异步控制方法、设备及存储介质。


背景技术：

2.电力系统是一个强非线性、高维数以及分层分布的动态系统，其网架结构、线数参数以及负荷分布等对于系统运行有着很大影响。任何干扰因素都可能造成系统的振荡、不稳定甚至崩溃。由此可见，保证电力系统的稳定运行，是电力系统最重要的任务，确保系统在遭受干扰后能够恢复到可以容许的平衡状态。
3.随着电力系统相关领域的快速发展，电力系统中延迟、碰撞以及拥塞等现象总是不可避免的发生，再加之系统容易受到非线性扰动的影响，可能无法实时处理海量数据进而导致性能降低。电力系统通过共享网络将空间分布的不同部件连接起来，带来方便的同时也伴随着安全隐患。由于电力系统各部件之间的网络链接是开放的，所以容易受到网络攻击。网络攻击主要分为三类：拒绝服务攻击、欺骗攻击和重放攻击。其中，欺骗攻击是一种重要的网络攻击，又称虚假数据注入攻击。典型的欺骗攻击者可以捕获传感器节点，利用未经授权的特权注入恶意代码或修改程序，从而降低甚至恶化系统性能。马尔科夫跳变系统由于其在结构突变物理系统中的建模优越性，将马尔科夫跳变系统理论应用于电力系统已成为控制领域的一个重要研究课题。
4.随机跳变系统的转移概率矩阵主要受限于停留时间的概率分布函数。对于马尔科夫跳变系统，驻留时间的概率分布函数服从指数/几何分布，根据无记忆特性，转移概率与驻留时间无关。但许多工业过程很难满足这种严格的限制条件，驻留时间遵循其他一些非指数/几何分布，在这种情况下，相应的随机跳变系统称为半马尔科夫跳变系统。由于非指数/几何分布的特性，半马尔科夫跳变系统的转移概率与驻留时间相关。使半马尔科夫跳变系统具有较小的保守性，可适用于更广泛的实际系统。
5.在运用传统马尔科夫链分析控制系统时，常常假设系统模态完全已知，然而这一理想假设在实际中是很难实现的。因而，提出了隐马尔科夫链概念，隐马尔科夫链可以看做是两层的参数过程：上层为传统的齐次马尔科夫链；下层为观测模态序列，其中上层马尔科夫链的模态无法直接观测到。观测模态序列由观测模态组成，并且运用该序列可对上层马尔科夫链中的模态进行估计。基于特殊的双层结构，隐马尔科夫链作为一类重要的统计模型被应用到众多实际系统。结合半马尔科夫链和隐马尔科夫链的优点，将隐马尔科夫链的上层随机过程替换为半马尔科夫链，从而引入隐半马尔科夫概念，并对隐半马尔科夫跳变系统进行稳定性分析与控制器设计。
6.综上所述，研究欺骗攻击下电力系统的异步控制方法，通过建立观测模态相关的控制器使电力系统在欺骗攻击下稳定运行是一个亟需解决的问题。


技术实现要素：

7.本发明为解决上述的问题，第一方面提供了一种多模态电力系统的异步控制方法，其方案步骤如下：
8.建立多模态电力系统的离散时间隐半马尔科夫跳变系统；
9.根据离散时间隐半马尔科夫跳变系统，设计依赖驻留时间的模态转移概率；
10.根据所设计的模态转移概率，确定观测模态的发射概率；
11.根据多模态电力系统受欺骗攻击影响，建立欺骗攻击模型；
12.基于离散时间隐半马尔科夫跳变系统和欺骗攻击模型，设计观测模态依赖的异步控制器；
13.根据所设计的观测模态依赖的异步控制器，确定异步控制器参数。
14.所述方法针对电力系统随机发生的欺骗攻击，建立异步机制下多模态电力系统的动态模型，设计出电力系统的异步控制策略，保证电力系统的稳定性。
15.在第一方面的一些实现方式中，所述建立多模态电力系统的离散时间隐半马尔科夫跳变系统为：
[0016][0017]
其中，z(k)∈rn表示系统状态，u(k)∈rm表示控制输入，为矩阵系数，{q(k),k≥0}是一个离散时间半马尔科夫链，在中取值。
[0018]
在第一方面的一些实现方式中，所述根据离散时间隐半马尔科夫跳变系统，设计依赖驻留时间的模态转移概率，包括：
[0019]
定义为在第次跳变与第次跳变之间的驻留时间，且是第次跳变的时刻，且k0＝0,是第次跳变时的系统所处模态；
[0020]
给定矩阵为离散时间半马尔科夫核，模态的转移概率且依赖驻留时间并满足
[0021][0022]
其中，δ
ην
是驻留时间概率密度函数。
[0023]
在第一方面的一些实现方式中，所述根据所设计的模态转移概率，确定观测模态的发射概率，包括：
[0024]
定义依赖当前模态和下一模态的驻留时间的转移概率密度函数为：
[0025][0026]
引入表示系统在当前模态的停留时间，并且观测模态在有限集合中取值；
[0027]
对于任意系统模态假设存在一个有限集合且其中h
η
≥1表示在该子集中元素的个数，
[0028]
确定所述观测模态的发射概率为：
[0029][0030][0031]
其中，表示为当系统模态为q(k)＝η时第次观测模态，为发射概率矩阵。
[0032]
在第一方面的一些实现方式中，所述根据多模态电力系统受欺骗攻击影响，建立欺骗攻击模型为：
[0033]zζ
(k)＝z(k) ζ(k)(-z(k) θ(k))，
[0034]
其中，z
ζ
(k)为欺骗攻击影响下的实际信号，z(k)表示系统状态，θ(k)为欺骗攻击信号，且在已知正常数条件下满足随机变量ζ(k)服从伯努利分布
[0035][0036][0037]
当ζ(k)＝0时，实际控制输入信号在系统中成功传输；当ζ(k)＝1时，欺骗攻击信号代替实际控制输入信号。
[0038]
在第一方面的一些实现方式中，所述基于离散时间隐半马尔科夫跳变系统和欺骗攻击模型，设计观测模态依赖的异步控制器为：
[0039][0040]
其中，为异步控制器的增益矩阵，使得离散时间隐半马尔科夫跳变系统是稳定的；z
ζ
(k)为欺骗攻击影响下的实际信号；u(k)∈rm表示控制输入。
[0041]
在第一方面的一些实现方式中，所述离散时间隐半马尔科夫跳变系统在欺骗攻击下的闭环系统为：
[0042][0043]
其中，z(k)∈rn表示系统状态，u(k)∈rm表示控制输入，z
ζ
(k)为欺骗攻击影响下的实际信号，θ(k)为欺骗攻击信号，为异步控制器的增益矩阵，为矩阵系数，当q(k)＝η时，ζ(k)为服从伯努利分布的随机变量
[0044]
进一步的，所述根据所设计的观测模态依赖的异步控制器，确定异步控制器参数，包括：
[0045]
存在一个标量对称矩阵矩阵矩阵当时，满足不等式方程
[0046]
[0047][0048]
其中，
[0049][0050][0051][0052][0053][0054][0055][0056][0057][0058][0059]
根据得到的矩阵确定异步控制器的增益矩阵
[0060]
第二方面提供了一种多模态电力系统的异步控制设备，包括处理器和存储器，所述处理器执行所述存储器中保存的程序数据时实现多模态电力系统的异步控制方法。
[0061]
第三方面提供了一种可读介质，用于存储控制程序数据，其中，所述控制程序数据被处理器执行时实现多模态电力系统的异步控制方法。
[0062]
本发明的有益效果在于：
[0063]
通过隐半马尔科夫模型来描述异步机制下多模态电力系统模型，具有强混杂性、随机性和模态非同步性，能够较好地描述其动力学特性；
[0064]
利用系统跳变模态的可用信息和欺骗攻击发生的概率信息设计观测模态相关的异步控制律保证电力系统的稳定性，并精确描述异步机制下多模态电力系统的动态特性，有效抑制欺骗攻击对电力系统的影响，解决多模态电力系统的异步控制问题，提高电力系统的安全性能。
附图说明
[0065]
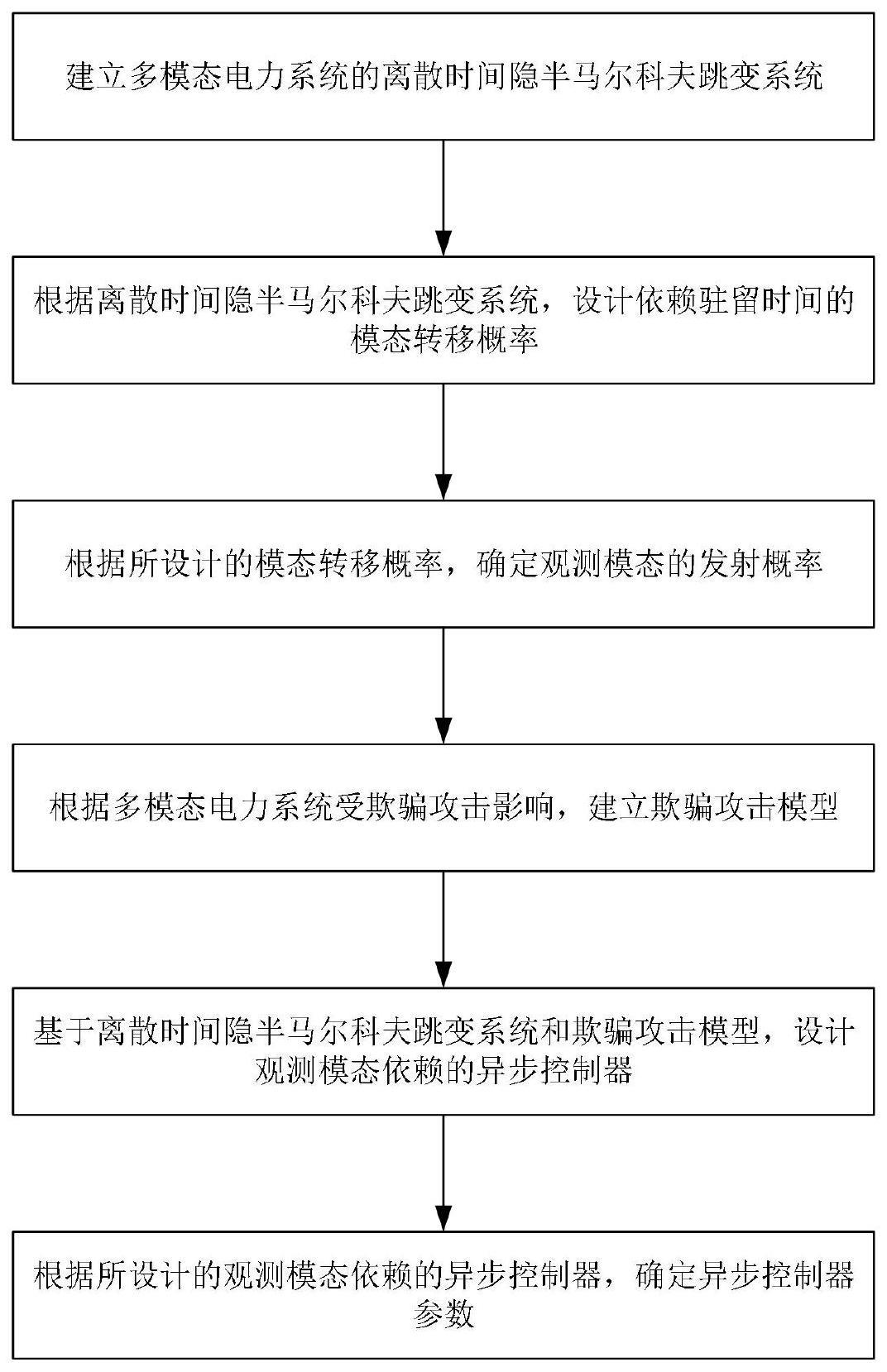
图1为一种多模态电力系统的异步控制方法流程图；
[0066]
图2为欺骗攻击下控制输入图；
[0067]
图3为电力系统的状态轨迹图。
具体实施方式
[0068]
下面将结合附图更详细地描述本公开的示例性实施方式。
[0069]
实施例
[0070]
参见图1，本发明提供了一种多模态电力系统的异步控制方法，具体实现步骤如下：
[0071]
步骤一：建立多模态电力系统的离散时间隐半马尔科夫跳变系统；
[0072]
所述多模态电力系统主要考虑连接至无限总线的单机，无限总线显示为大型互连电力系统的thevenin等效电路，根据无限总线单机电力系统，建立动力学模型为：
[0073][0074][0075][0076][0077]
其中，变量说明如下表所示：
[0078][0079][0080]
根据动力学模型建立多模态电力系统的状态空间方程为：
[0081][0082]
[0083][0084][0085]
其中，z(t)表示系统状态，u(t)表示控制输入，为矩阵系数，δδ，δω分别为转子角的偏差、转子相对转速的偏差，δe'q，δe
fd
分别为q轴瞬态电动势的偏差、发电机励磁电压的偏差，k1,k2,k3…
k6为同步电机的线性化模型常数。
[0086]
进一步的，所研究系统的参数取值如下：
[0087]
1)同步电机参数：x'd＝0.32pu，xd＝1.6pu，xq＝1.55pu,t'
do
＝6s，xe＝0.4pu，m＝10s，ω0＝π
×
50rad/s；
[0088]
2)励磁机放大器参数：ke＝50，te＝0.05s；
[0089]
3)线路电抗：l1＝l2＝0.8。
[0090]
根据所述状态空间方程，将电力系统的随机拓扑变化用半马尔科夫链表示，建立多模态电力系统的离散时间隐半马尔科夫跳变系统：
[0091][0092]
其中，z(k)∈rn表示系统状态，u(k)∈rm表示控制输入，为矩阵系数，{q(k),k≥0}是一个离散时间半马尔科夫链，在中取值。
[0093]
根据上述参数取值，得到和的拟合数据如下：
[0094][0095][0096][0097][0098]
步骤二、根据离散时间隐半马尔科夫跳变系统，设计依赖驻留时间的模态转移概
率；
[0099]
定义为在第次跳变与第次跳变之间的驻留时间，且是第次跳变的时刻，且k0＝0,是第次跳变时的所述系统的所处模态；
[0100]
给定矩阵为离散时间半马尔科夫核，模态的转移概率且依赖驻留时间并满足
[0101][0102]
其中，δ
ηv
是驻留时间概率密度函数。
[0103]
步骤三、根据所设计的模态转移概率，确定观测模态的发射概率；
[0104]
定义依赖当前模态和下一模态的驻留时间的转移概率密度函数为：
[0105][0106]
考虑其中模态转移概率ξ
12
＝1,ξ
21
＝1,概率密度函数驻留时间上界为
[0107]
引入表示系统在当前模态的停留时间，并且所述当前模态的停留时间不依赖于跳变次数依赖于采样时间k；观测模态在有限集合中取值；
[0108]
对于任意系统模态假设存在一个有限集合且其中h
η
≥1表示在该子集中元素的个数，
[0109]
确定所述观测模态的发射概率为：
[0110][0111][0112]
其中，表示为当系统模态为q(k)＝η时第次观测模态，为发射概率矩阵。
[0113]
进一步的，所述发射概率矩阵根据驻留时间拟合数据为：
[0114][0115]
步骤四：根据多模态电力系统受欺骗攻击影响，建立欺骗攻击模型为：
[0116]zζ
(k)＝z(k) ζ(k)(-z(k) θ(k))
[0117]
其中，z
ζ
(k)为欺骗攻击影响下的实际信号，θ(k)为欺骗攻击信号，且在已知正常数条件下满足
[0118]
ζ(k)为随机变量并且符合伯努利分布：ζ(k)为随机变量并且符合伯努利分布：当ζ(k)＝0时，实际控制输入信号在系统中成功传输；当ζ(k)＝1时，欺骗攻击信号代替实际控制输入信号。
[0119]
进一步得到欺骗攻击模型参数为
[0120]
根据欺骗攻击模型，得到所述离散时间隐半马尔科夫跳变系统在欺骗攻击下的闭环系统为：
[0121][0122]
其中，z(k)∈rn表示系统状态，u(k)∈rm表示控制输入，z
ζ
(k)为欺骗攻击影响下的实际信号，θ(k)为欺骗攻击信号，为异步控制器的增益矩阵，为矩阵系数，当q(k)＝η时，ζ(k)为服从伯努利分布的随机变量。
[0123]
步骤五：基于离散时间隐半马尔科夫跳变系统和欺骗攻击模型，设计观测模态依赖的异步控制器；
[0124]
所述观测模态依赖的异步控制器公式如下：
[0125][0126]
其中，为异步控制器的增益矩阵，使得离散时间隐半马尔科夫跳变系统是稳定的；z
ζ
(k)为欺骗攻击影响下的实际信号；u(k)∈rm表示控制输入。
[0127]
步骤六：根据所设计的观测模态依赖的异步控制器，确定异步控制器参数；
[0128]
对任意多模态电力系统模态和观察模态存在一个标量对称矩阵矩阵矩阵当时，满足不等式方程
[0129][0130][0131]
其中，
[0132][0133][0134][0135]
[0136][0137][0138][0139][0140][0141][0142]
根据确定的离散时间半马尔科夫核、发射概率矩阵和欺骗攻击模型参数，可以得到矩阵确定满足系统稳定性目标的异步控制器的增益矩阵
[0143][0144][0145]
如图2、图3所示，图2表明了本发明所提出的异步控制器其控制输入，在欺骗攻击下收敛至原点；图3表明了电力系统的状态轨迹在异步控制方法下达到平衡点，从而可以有效抑制欺骗攻击对电力系统的影响，提供电力系统的安全性。
[0146]
此外，本发明提供了一种多模态电力系统的异步控制设备，包括处理器和存储器，所述处理器执行所述存储器中保存的程序数据时实现所述的一种多模态电力系统的异步控制方法。
[0147]
最后，本发明提供了一种可读介质，用于存储控制程序数据，其中，所述控制程序数据被处理器执行时实现所述的一种多模态电力系统的异步控制方法。