一种飞行汽车人机共驾的驾驶权交互决策方法-j9九游会真人

1.本发明属于智能驾驶技术领域，特别是涉及一种飞行汽车人机共驾的驾驶权交互决策方法。


背景技术：

2.为减轻日益增长的城市交通压力，新型的运输航空器的使用正受到越来越多的关注，其中包括了飞行汽车以及evtol(electric vertical takeoff and landing)飞行器等新概念航空器。通常，飞行汽车有三种控制模式：人工驾驶(hp)、自动驾驶(sp)和混合驾驶。在hp模式下，飞行汽车由飞行员驾驶，就像传统的飞机一样，需要驾驶执照或飞行员证书。在sp模式下，飞行汽车可以以完全自主的方式执行所有操作，而不需要飞行员，因此与hp模式相比，运行成本更低。混合驾驶模式已被开发中的一些飞行汽车提出并采用，以充分利用上述两种控制模式的单独优势。从长远来看，混合模式成本虽高，但不可否认这必然是新型航空器最安全的选择。
3.混合模式需要自动驾驶系统与驾驶人协同参与驾驶，也称为人机共驾模式。根据控制权作为划分依据，人机共驾技术可以划分为两种模式：双驾单控模式和双驾双控模式。双驾单控模式指某一方同时控制车辆的横向运动和纵向运动，其主要关注点是驾驶权的切换问题；双驾双控指车辆负责纵向控制，驾驶人负责横向控制，其主要关注点是驾驶自信问题。在人机共驾模式下，涉及人机交互中的双驾单控模式下的驾驶权交互问题就显得尤为重要。该问题的核心在于驾驶过程中的不确定性，包括车辆状态不确定性、驾驶人的不确定性以及环境的不确定性等。从目前来看，驾驶员因素、车辆因素和周围环境因素等在内的诸多交通因素构成的驾驶环境风险对于驾驶权是否有条件切换有着决定性的影响。
4.因此，需要一种飞行汽车人机共驾的驾驶权交互决策建模方法，能够针对复杂的驾驶环境进行安全的驾驶权交互决策。


技术实现要素：

5.本发明的目的是提供一种飞行汽车人机共驾的驾驶权交互决策方法，用以解决在危险情况下双驾单控过程中驾驶权是否有条件从智能驾驶系统控制切换到驾驶员控制的问题。
6.为实现上述目的，本发明提供了一种飞行汽车人机共驾的驾驶权交互决策方法，包括以下步骤：
7.获取影响飞行汽车驾驶安全的车辆信息、驾驶员信息、环境信息和交通信息；
8.基于所述车辆信息、驾驶员信息、环境信息和交通信息，获得对应的车辆控制指标、驾驶员身体指标、驾驶过程中的环境因素、驾驶过程中飞行汽车状况和驾驶员水平；
9.基于所述车辆控制指标和驾驶员身体指标，分别构建对应的车辆动态风险模型以及驾驶员动态风险模型，并得到车辆动态风险指数以及驾驶员动态风险指数；
10.基于所述车辆动态风险指数、驾驶员动态风险指数以及驾驶过程中的环境因素、
驾驶过程中飞行汽车状况和驾驶员水平，构建驾驶员交互决策模型，并对所述驾驶员交互决策模型进行优化；
11.基于优化后的驾驶员交互决策模型，获得驾驶权交互决策结果。
12.可选地，获得车辆动态风险指数的过程包括：基于车辆控制指标，采用模糊认知图，构建车辆动态风险模型；对所述车辆动态风险模型的初始权重采用多专家加权确定，获得车辆动态风险模型的初始关联权值矩阵，进而获得车辆动态风险指数；
13.其中，所述车辆控制指标包括：车辆距离控制指标、车辆加速度控制指标和方向盘转向控制指标。
14.可选地，获得驾驶员动态风险指数的过程包括：基于驾驶员身体指标，采用模糊认知图，构建驾驶员动态风险模型；对所述驾驶员动态风险模型的初始权重采用多专家加权确定，获得驾驶员动态风险模型的初始关联权值矩阵，进而获得驾驶员动态风险指数；
15.其中，所述驾驶员身体指标包括：驾驶员眼睛闭合指标、驾驶员眨眼频率、驾驶员视线转移时间、驾驶员脑电指标和驾驶员心电指标。
16.可选地，所述驾驶权交互决策模型的构建过程包括：预设交互决策指数，基于模糊认知图，对车辆动态风险指数、驾驶员动态风险指数、驾驶过程中的环境因素、驾驶过程中飞行汽车状况和驾驶员水平进行因果推理，获得所述车辆动态风险指数、驾驶员动态风险指数、驾驶过程中的环境因素、驾驶过程中飞行汽车状况和驾驶员水平与交互决策指数之间的关系，进而获得驾驶权交互决策模型。
17.可选地，对所述驾驶权决策交互模型进行优化之前还包括：基于专家加权法，对所述驾驶权决策交互模型的初始权重进行加权，并运用模糊逻辑将专家的语言评级转换为数字权重，获得驾驶权决策交互模型的初始关联权值矩阵。
18.可选地，对所述驾驶权决策交互模型进行优化的过程包括：对驾驶权决策交互模型的初始关联权值矩阵进行评估，若满足预设条件，则获得最优的关联权值矩阵；否则对初始关联权重矩阵进行交叉、变异，依此反复迭代，直到满足预设条件，选择适应度最高的关联权重矩阵为最优的关联权值矩阵。
19.可选地，基于优化后的驾驶员交互决策模型进行决策的过程包括：引入直觉模糊集，获得第一决策阈值和第二决策阈值；当交互决策指数的状态值小于第一决策阈值时，输出驾驶员不接管的决策结果，当所述交互决策指数的状态值大于第二决策阈值时，输出驾驶员接管的决策结果，当所述交互决策指数的状态值在所述第一决策阈值和第二决策阈值之间时，输出驾驶员辅助决策结果。
20.可选地，获得第一决策阈值和第二决策阈值的过程包括：基于所述直觉模糊集获取驾驶事件属于所述直觉模糊集的隶属度和非隶属度，基于所述隶属度和非隶属度，获得驾驶事件属于所述直觉模糊集的不确定程度；基于所述驾驶员交互决策模型的迭代次数，获得迭代后的隶属度、非隶属度和不确定程度；基于迭代后的隶属度、非隶属度和不确定程度，构建成本型指标损失函数矩阵和效益型指标损失函数矩阵；基于逆泊松分布法将所述成本型指标损失函数矩阵和效益型指标损失函数矩阵进行融合，获得融合后的损失函数矩阵；基于所述融合后的损失函数矩阵，获得第一决策阈值和第二决策阈值。
21.本发明的技术效果为：
22.本发明针对真实复杂的驾驶环境，将驾驶权切换问题与驾驶环境风险问题相结
合，有效的解决了自动驾驶系统接管到驾驶员接管的切换这一包含诸多不确定性影响因素的动态问题，构建的驾驶员交互决策模型具备较高的准确性和实时性，保证了人机共驾下的驾驶权切换过程中人员和飞行汽车的安全性。
附图说明
23.构成本技术的一部分的附图用来提供对本技术的进一步理解，本技术的示意性实施例及其说明用于解释本技术，并不构成对本技术的不当限定。在附图中：
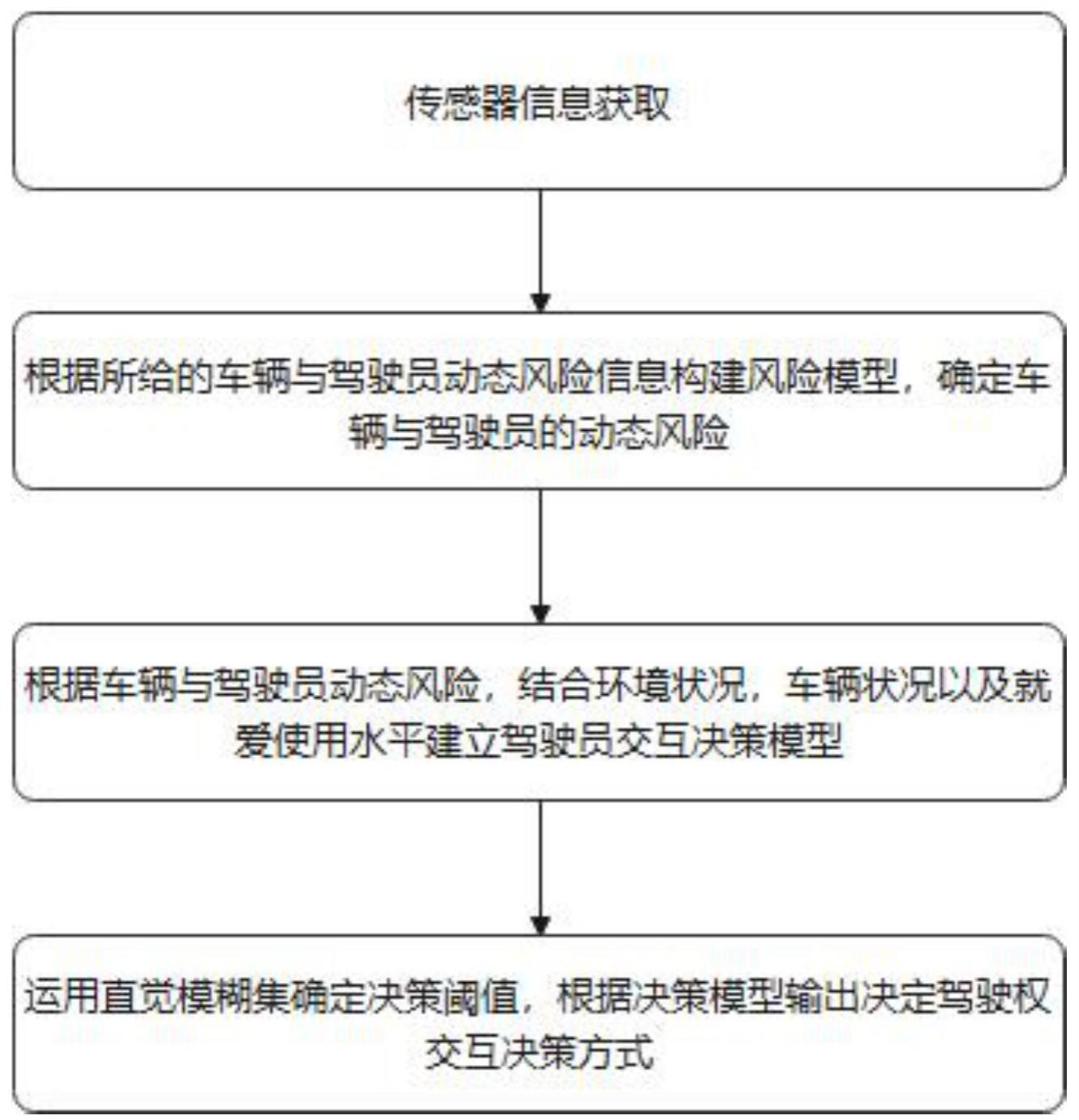
24.图1为本发明实施例中的飞行汽车人机共驾的驾驶权交互决策方法总体流程图；
25.图2为本发明实施例中的基于fcm的车辆动态风险模型图；
26.图3为本发明实施例中的基于fcm的驾驶员动态风险模型图；
27.图4为本发明实施例中的基于fcm的驾驶权交互决策模型图；
28.图5为本发明实施例中的驾驶权交互决策关联矩阵训练流程图。
具体实施方式
29.需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。下面将参考附图并结合实施例来详细说明本技术。
30.需要说明的是，在附图的流程图示出的步骤可以在诸如一组计算机可执行指令的计算机系统中执行，并且，虽然在流程图中示出了逻辑顺序，但是在某些情况下，可以以不同于此处的顺序执行所示出或描述的步骤。
31.实施例一
32.如图1所示，本实施例中提供一种飞行汽车人机共驾的驾驶权交互决策方法，如图1所示，包括以下步骤：
33.步骤1：在飞行汽车内外布置传感器，使传感器能获取前后车辆距离、周围交通流信息、加速度、方向盘转角、驾驶员眼动信息、驾驶员心电信息以及驾驶员脑电信息。
34.步骤2：获取传感器采集的影响飞行汽车驾驶安全的信息。本实施例中，影响飞行汽车驾驶安全的信息包括车辆信息、驾驶员信息、环境信息和交通信息。
35.所述飞行汽车车辆信息至少包括车辆速度、加速度、方向盘转向熵、车辆状况；驾驶员信息至少包括闭眼率、眨眼频率、视线转移时间、脑电指标、心电指标、驾驶员水平；环境信息至少包括外部天气情况、能见度等，交通信息至少包括车辆距离、交通流状况等。
36.步骤3：根据传感器所获取信息，定义模型的输入变量，包括车辆控制指标、驾驶员身体指标、驾驶过程中的环境因素、驾驶过程中飞行汽车状况和驾驶员水平；其中，所述车辆控制指标包括：车辆距离控制指标、车辆加速度控制指标和方向盘转向控制指标，所述驾驶员身体指标包括：驾驶员眼睛闭合指标、驾驶员眨眼频率、驾驶员视线转移时间、驾驶员脑电指标和驾驶员心电指标。具体获取过程如下所示：
37.步骤3-1，计算车辆距离控制指标c1，车辆距离控制指标c1主要考虑不同速度下的车辆间距。车辆制动过程中，开始制动前两车分别位于xi，x
i-1
位置，车辆间距为d。前车开始制动，车辆制动行驶距离为后车在反应时间τ内行驶的距离为vi(t)τ，制动过程
中行驶距离为可得公式：
[0038][0039]
车辆间距为：
[0040][0041]
式中：vi为制动过程开始前第i辆车的行驶速度；αi为第i辆车的最大制动减速度；τ为驾驶员反应时间和制动器生效时间总和；d为两车停下后的最小间距。
[0042]
假设两车初始速度相同，且制动效果相同，则最小车辆间距为：d
min
＝vi(t)τ d，据相关数据表明，驾驶员平均反应时间为0.8s，而制动效果时间为0.2s，d＝1m可视为安全。根据上述可计算出不同车速下的最小车辆间距。
[0043]
将最小车辆间距与实际车辆间距的比作为动态风险中车距因素的指标：
[0044][0045]
其中d表示实际驾驶过程中两车的距离，d
min
表示两车最小安全间距，ζ反映车距动态风险；
[0046]
步骤3-2，计算车辆加速度控制指标c2，取加速度a的绝对值|a|作为反映车辆加速度的控制指标；
[0047]
步骤3-3，计算方向盘转向控制指标c3，表征车辆行驶过程中的转向控制能力。在每个时间点t，利用二阶泰勒展开，根据之前方向盘转角角度θ预测转向角，如下述公式：预测误差e(t)为：e(t)＝θ(t)-θ
p
(t)。在实际驾驶过程中，计算出车辆驾驶判断错误的方向盘操作数据，将收集到的数据进行正态分布处理，将预测偏差划分为9个区间，根据方向盘转角值在各个区间内的频数确定各区间分布概率，计算每个区间的误差概率值，获得转向熵值：pi为每个区间的概率。
[0048]
步骤3-4，计算驾驶员眼睛闭合指标c5，采用perclos(percentage of eye closure)方法。t
close
为时间t内眼睛闭合总时间。
[0049]
步骤3-5，计算驾驶员眨眼频率c6，即单位时间内驾驶员眼睛的闭合睁开次数。
[0050]
步骤3-6，计算驾驶员视线转移时间c7，即驾驶员视线离开前方视野的时间。
[0051]
步骤3-7，计算驾驶员脑电指标c8，采用脑电波θ波与β波的频率之比η。
[0052]
步骤3-8，计算驾驶员心电指标c9，采用rr间期(心脏每次搏动间期)标准差(sdnn)。
[0053]
步骤3-9，定义驾驶过程中的环境因素c
11
，将天气是否正常，交通流是否拥挤，能见
度高低，路线复杂程度等考虑在内，定义环境因素为三个状态：外部环境状况良好为0.8，外部环境状况一般为0.5，外部环境差为0.3。
[0054]
步骤3-10，定义驾驶过程中飞行汽车状况c
12
，将行驶里程、行驶系统状态、转向系统状态、制动系统状态、发动机状况等考虑在内，定义飞行汽车状况为三个状态：飞行汽车状况良好为0.7，车辆状况一般为0.5，车辆状况差为0.3。
[0055]
步骤3-11，定义驾驶员水平c
13
，将心理素质、驾龄、视力情况、睡眠质量、是否吃药等考虑在内，定义驾驶员水平为三个状态：驾驶员水平良好为0.7，驾驶员水平一般为0.5，驾驶员水平差为0.3。
[0056]
步骤3-12，定义c4表示车辆动态风险指数，c
10
表示驾驶员动态风险指数，c
14
表示交互决策指数。
[0057]
步骤4：建立基于模糊认知图(fcm)的车辆动态风险模型。
[0058]
步骤4-1，如图2所示，根据因果推理，构建基于fcm的车辆动态风险模型：
[0059]
步骤4-2，对基于fcm的车辆动态风险模型的初始权重采用多专家加权确定，专家运用语言术语(例如：非常高、高、低)表达因素之间的因果关系，随后根据专家的专业程度、经验年限等因素，加权运用模糊逻辑将语言评级转换为数字权重，最终确定初始关联权值矩阵。
[0060]
步骤4-3，根据所确定的关联权值矩阵，结合所得车辆动态风险模型,推理计算得到车辆动态风险模型的输出节点车辆动态风险c4状态值。
[0061]
步骤5：建立基于fcm的驾驶员动态风险模型。
[0062]
步骤5-1，如图3所示，根据因果推理，构建基于fcm的驾驶员动态风险模型：
[0063]
步骤5-2，对基于fcm(模糊认知图)的驾驶员动态风险模型的初始权重采用上述步骤4-2方法，最终确定的初始关联权值矩阵。
[0064]
步骤5-3，根据所确定的关联权值矩阵，结合所得驾驶员动态风险模型,推理计算得到驾驶员动态风险模型的输出节点驾驶员动态风险c
10
状态值。
[0065]
步骤6：根据车辆动态风险模型以及驾驶员动态风险模型所得输出节点车辆动态风险指数和驾驶员动态风险指数，以及环境因素、车辆状况、驾驶员水平，构建基于fcm的驾驶权交互决策模型，并引入基于直觉模糊集的决策阈值算法对决策模型进行决策，引入基于实数编码的遗传算法(rcga)对决策模型进行优化。
[0066]
步骤6-1，如图4所示，根据因果推理，构建基于fcm的驾驶权交互决策模型：
[0067]
步骤6-2，对基于fcm的驾驶权交互决策模型的初始权重采用上述步骤4-2方法，最终确定的初始关联权值矩阵。
[0068]
步骤6-3，对交互决策模型中的初始权重使用rcga进行优化，对初始化群体中的染色体边权矩阵(决策模型初始关联权值矩阵)进行评估，即将经fcm概念节点状态变换产生下一时刻fcm概念节点状态值与时序数据源中的实际结果进行比较，若达到结束条件，则获得了最优的fcm边权矩阵，否则对染色体权重矩阵进行交叉、变异，并从中选择出适应度高的染色体权重矩阵生成新一代的群体进入下一轮的判定，依此反复迭代，直到满足结束条件为止。其中根据fcm计算得到的新状态与在该时刻实际的状态值进行比较，可以得到fcm的误差函数：式中，an(t)为节点n在t时刻的实际状态，an
(t)为节点n在t时刻fcm计算得到的状态。适应度函数可以由误差函数来定义：具体流程图如图5所示。
[0069]
步骤6-4，经过模型因果推理结合优化后的关联权值矩阵得到交互决策指数状态值。
[0070]
步骤6-5，引入直觉模糊集，确定决策阈值α和β的大小。
[0071]
步骤6-5-1，设x为给定的有限非空论域，阈值设定为：0≤β≤α≤1，通过阈值将论域x分为pos(a)、bnd(a)、neg(a)3个区域。pos(a)表示交互决策节点c
14
状态值不小于α，执行驾驶员接管的决策结果。bnd(a)表示交互决策节点c
14
状态值介于β和α之间，执行驾驶员辅助决策的决策结果。neg(a)表示交互决策节点c
14
状态值不大于β，执行驾驶员不接管的决策结果。
[0072]
设定决策理论集由状态集和行为集构成，代表驾驶事件的状态集，表示一个驾驶事件是否属于集合a；ac＝(a
p
,ab,an)代表行为集，a
p
代表x∈pos(a)，ab代表x∈bnd(a)，an代表x∈neg(a)。如表1所示，λ
pp
、λ
bp
、λ
np
代表当驾驶事件属于a时采取a
p
、ab、an行为的损失函数；λ
pn
、λ
bn
、λ
nn
代表当驾驶事件属于时采取a
p
、ab、an行为的损失函数，如表1所示。
[0073]
表1
[0074][0075]
步骤6-5-2，设u是一个给定的非空集合，则称u上的一个直觉模糊集a：a＝{《x,μa(x),va(x)》|x∈u}
[0076]
式中：μa(x)和va(x)分别为非空集合u中元素x属于a的隶属度和非隶属度。
[0077]
其中
[0078]
μa(x):u
→
[0,1],x∈u|
→
μa(x)∈[0,1]
[0079]
va(x):u
→
[0,1],x∈u|
→
va(x)∈[0,1]
[0080]
且对于a上的所有x∈u，0≤μa(x) va(x)≤1都成立。
[0081]
则有πa(x)＝1-μa(x)-va(x)，式中：πa(x)为元素x属于a的犹豫度，用来描述元素x是否属于集合a的不确定程度。对于任意的x，有0≤πa(x)≤1。
[0082]
步骤5-5-3，构建一个n1×
n2的。n1为交互决策模型的节点个数，n2为交互决策模型推理迭代次数。矩阵元素由组成，其中隶属度为第i1个节点的第j1次迭代推理后的状态值，选定一个犹豫度后，即可计算得到非隶属度
[0083]
步骤6-5-4，将交互决策模型的输入指标节点分为成本型指标和效益型指标两类，并分别构建损失函数矩阵。
[0084]
成本型指标损失函数矩阵：
[0085][0086]
效益型指标损失函数矩阵：
[0087][0088]
其中：σ为自适应风险规避系数，公式为其中：
[0089]
步骤6-5-5，对不同时刻进行时间序列赋权，采用逆泊松分布法确定不同时刻的时间序列权值，计算直觉模糊决策矩阵中所有元素的损失函数矩阵并根据时间序列进行赋权，进而得到动态融合后的损失函数矩阵。
[0090][0091]
其中：ηk≥0，φ为泊松分布参数，0＜φ＜2。
[0092]
步骤6-5-6，基于贝叶斯最小风险理论求得对应的决策阈值：
[0093][0094][0095]
步骤6-5-7，对比c
14
状态值与决策阈值α和β的大小，输出最终的交互决策结果。
[0096]
步骤6-6，比较交互决策节点状态值与决策阈值α和β的大小，输出最终的交互决策结果。当节点状态值小于β时，输出驾驶员不接管的决策结果；当节点状态值大于α时，输出驾驶员接管的决策结果；当节点状态值在β与α之间时，输出驾驶员辅助决策结果。
[0097]
以上所述，仅为本技术较佳的具体实施方式，但本技术的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本技术揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本技术的保护范围之内。因此，本技术的保护范围应该以权利要求的保护范围
为准。