一种基于高速状态转换模型的agv队列的避撞控制方法-j9九游会真人

一种基于高速状态转换模型的agv队列的避撞控制方法
技术领域
1.本发明属于自动控制领域，具体涉及一种基于高速状态转换模型的agv队列的避撞控制方法，以及对应的避撞控制器。


背景技术：

2.随着自动控制和人工智能的技术不断进步，各种无人车和无人机已经逐渐开始商业化应用，并取代人工完成部分传统的重复性劳动；例如无人机配送，和码头的agv货运小车等。在这些领域中，前沿的技术是各类多智能体集群控制技术。
3.队列系统是多智能体集群控制中的一个分支。队列系统脱胎于多智能体系统，核心技术是纵向跟随技术，其目的是根据不同的编队要求和环境约束，将具有类似行驶特征的零散车辆变成一个队列行驶，或将零散车辆编入已有队列中行驶，或在车辆驶离、驶入队列后重新编组为新的队列系统。在过去的30年里已经取得了较为丰硕的成果，其应用可见于高速公路系统、工业agv、智慧物流、军事领域。其关键技术包括车车通信(v2v)、路径规划、路径跟踪、稳定性控制等。
4.单个agv系统本身就是一个由多个子系统构成的复杂系统，由多个agv系统构成的agv队列系统则更加复杂。尽管当前在队列系统的纵向控制方面已经有很多研究成果，但对高速率避撞相关研究仍然较少。一方面，现有技术对非完整约束尤其是不等式约束条件下的队列系统建模研究较少，且在建模时未将避撞条件嵌入到模型中；因而通常无法实现有效的全局避撞。另一方面，现有的研究大部分仅对agv的动力学模型进行了简化处理，未能克服系统中存在的参数不确定性、外部干扰、通讯问题(如延迟、信息错误、数据丢失)等缺陷，这仍然能会对队列系统的稳定性造成巨大挑战；进而影响队列系统的控制精度和安全性。


技术实现要素：

5.为了解决现有的agv队列系统的控制精度不足，稳定性差，无法实现全局避撞的问题，本发明提供一种基于高速状态转换模型的agv队列的避撞控制方法，以及对应的避撞控制器。
6.本发明采用以下技术方案实现：
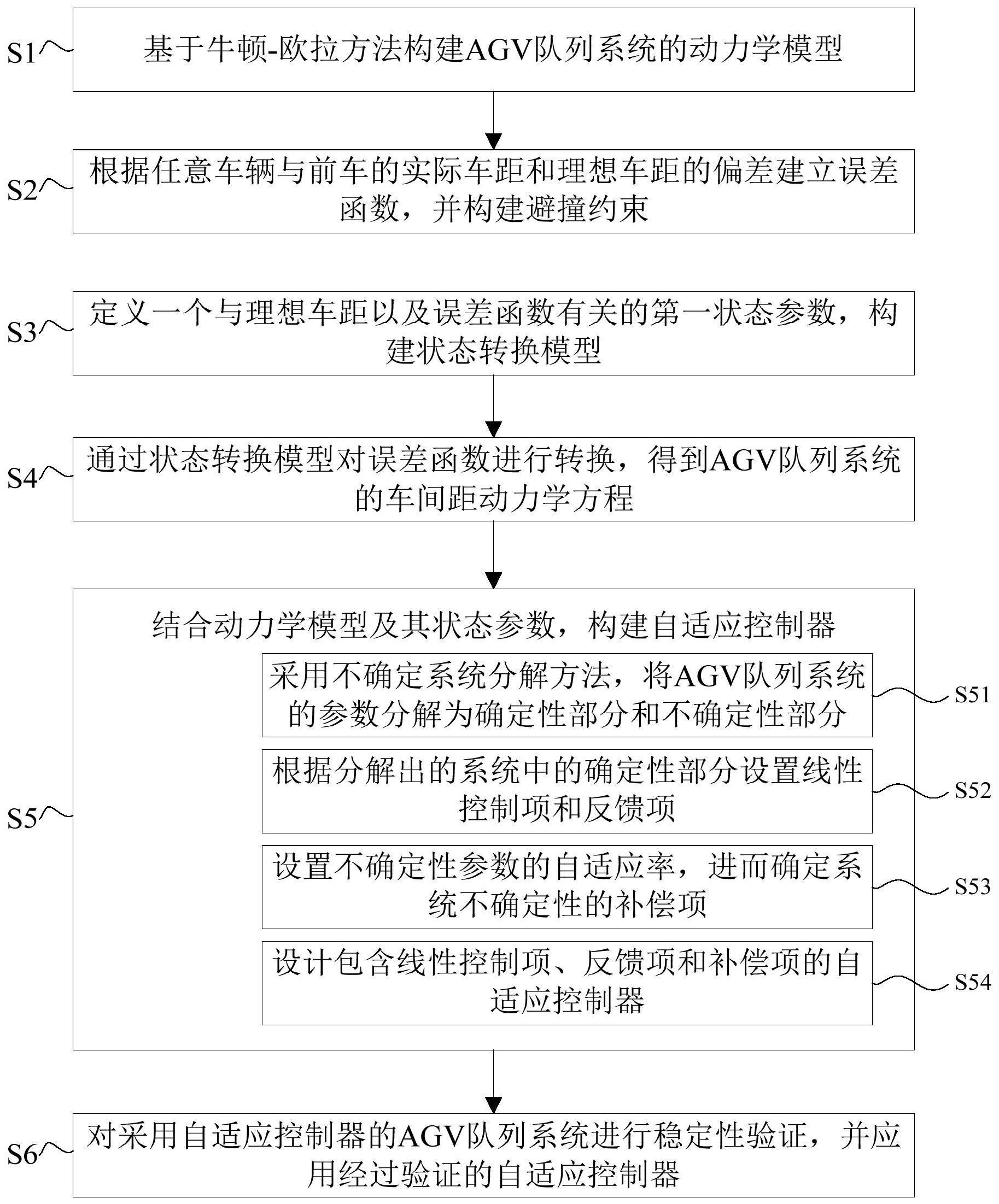
7.一种基于高速状态转换模型的agv队列的避撞控制方法，该避撞控制方法包括如下步骤：
8.s1：基于牛顿-欧拉方法构建agv队列系统的动力学模型。
9.s2：根据任意车辆与前车的实际车距si和理想车距的偏差建立误差函数ei(t)，并构建避撞约束。
10.s3：定义γ
i1
为一个与理想车距以及误差函数有关的第一状态参数，其对应的高速状态转换模型如下：
[0011][0012]
s4：通过高速状态转换模型对误差函数进行转换，得到agv队列系统的车间距动力学方程。
[0013]
s5：结合所述动力学模型以及车间距动力学方程中的状态参数，构建一个满足全局避撞约束的自适应控制器，包括如下步骤：
[0014]
s51：采用不确定系统分解方法，将agv队列系统的动力学模型中的参数分解为确定性部分和不确定性部分。
[0015]
s52：根据分解出的系统中的确定性部分设置线性控制项u
i1
和反馈项u i2
：
[0016][0017]
上式中，和分别表示第i个车辆的动力学模型中行驶阻力fi和质量mi的确定性部分；γ
i2
表示第二状态参数，表示第二状态参数，和分别为第一状态参数的二阶导数中误差函数的一阶系数和二阶系数；γ
i3
表示第三状态参数；
[0018]
s53：设置用于估计agv队列系统中的不确定性参数αi的自适应率，进而确定系统不确定性的补偿项u
i3
：
[0019][0020]
上式中，表示不确定性参数的估计值；表示不确定参数αi的估计函数；表示函数的补偿函数；表示与有关的调整系数；γi表示求和函数项数。
[0021]
s54：设计包含线性控制项u
i1
、反馈项u
i2
和补偿项u
i3
的自适应控制器；自适应控制器中的控制力输入ui为：
[0022]
ui＝u
i1
u
i2
u
i3
。
[0023]
s6：对采用自适应控制器的agv队列系统进行稳定性验证，并利用经过验证的自适应控制器实现agv队列系统的全局避障和稳定控制。
[0024]
作为本发明进一步的改进，步骤s1中，任意车辆的动力学方程如下：
[0025][0026]
上式中，t表示时间；χi表示车辆的位移；σi表示设计的不确定参数；ui表示控制力输入；mi表示第i辆车的质量；表示包括滚动阻力、加速阻力和其他外部干扰的行驶阻力的总和。
[0027]
作为本发明进一步的改进，步骤s2中，在初始安全条件下，任意车辆i与前车不发生碰撞的充要条件为：
[0028][0029]
上式中，表示第当前车辆i的前车的车身长度；
[0030]
误差函数为：
[0031][0032]
则agv队列系统的避撞约束为：
[0033][0034]
作为本发明进一步的改进，步骤s4中，agv队列系统满足车辆避撞的二阶约束为：
[0035][0036]
转换后的车间距动力学方程如下：
[0037][0038]
作为本发明进一步的改进，步骤s5中，一阶系数、二阶系数和第三状态参数分别满足：
[0039][0040][0041][0042]
作为本发明进一步的改进，在步骤s51agv队列系统的动力学模型中，系统参数分解如下：
[0043][0044]
上式中，和分别表示第i个车辆的行驶阻力和质量的确定性部分；δmi和δfi分别表示第i个车辆的行驶阻力和质量的不确定性部分。
[0045]
作为本发明进一步的改进，步骤s52中，控制力输入中的反馈项u
i2
满足：
[0046][0047]
上式中，βi为一个自适应反馈控制系数，且满足：
[0048][0049]
作为本发明进一步的改进，步骤s53中，不确定性参数αi的自适应律为：
[0050][0051]
上式中，k1表示偏微分系数；表示不确定参数估计值的估计函数：表示与第二状态参数相关的函数，k2表示估计值系数。
[0052]
作为本发明进一步的改进，估计函数函数的补偿系数满足：
[0053][0054]
本发明还包括一种ag队列系统的避撞控制器，其采用如前述的基于高速状态转换模型的agv队列的避撞控制方法中设计的自适应控制器；避撞控制器用于快速实现agv队列系统的队列成形和避撞控制。
[0055]
本发明提供的技术方案，具有如下有益效果：
[0056]
本发明针对agv队列系统提出了一种新的基于分段函数的高速状态转换模型，利用该模型可以将大幅简化控制系统的设计，并实现系统稳定性的快速收敛，进而使得控制系统具有高速率的特性。此外，基于重新设计的高速率高速状态转换模型，本发明还将避撞约束引入到了agv队列系统而非各个agv车辆中，进而实现了agv队列系统的全局避撞设计。本发明方案可以保证系统在行驶过程中不发生碰撞，并且可以保持在所规定的理想车距左右，从而可保证队列系统的紧凑性。
[0057]
本发明提供的控制方法及其自适应控制器与传统方案相比，具有收敛速度快，控制精度高，可实现全局避撞的特性，非常适合在agv队列系统控制中进行推广应用。
附图说明
[0058]
图1为本发明实施例1中提供的一种基于高速状态转换模型的agv队列的避撞控制方法的步骤流程图。
[0059]
图2为自动控制系统设计中一直有界性和一致最终有界性的原理示意图。
[0060]
图3为仿真实验中在条件下，三个车辆的位置变化曲线。
[0061]
图4为仿真实验中在ei≥0条件下，三个车辆的位置变化曲线。
[0062]
图5为仿真实验中在条件下，三个车辆的速度变化曲线。
[0063]
图6为仿真实验中在ei≥0条件下，三个车辆的速度变化曲线。
[0064]
图7为仿真实验中在条件下，车辆1、2，以及车辆2、3之间理想车距和实际车距的误差变化曲线。
[0065]
图8为仿真实验中在ei≥0条件下，车辆1、2，以及车辆2、3之间理想车距和实际车距的误差变化曲线。
[0066]
图9为仿真实验中在条件下，车辆2和3的控制力输入的变化曲线。
[0067]
图10为仿真实验中在ei≥0条件下，车辆2和3的控制力输入的变化曲线。
[0068]
图11为仿真实验中，在条件下，采用不同状态变换函数进行自适应控制时，车辆1和2的跟随误差的变化曲线对比。
[0069]
图12为仿真实验中，在ei≥0条件下，采用不同状态变换函数进行自适应控制时，车辆1和2的跟随误差的变化曲线对比。
[0070]
图13为仿真实验中，在条件下，采用不同状态变换函数进行自适应控制时，车辆2和3的跟随误差的变化曲线对比。
[0071]
图14为仿真实验中，在ei≥0条件下，采用不同状态变换函数进行自适应控制时，车辆2和3的跟随误差的变化曲线对比。
具体实施方式
[0072]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步地详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。
[0073]
实施例1
[0074]
传统agv队列系统进行避撞和稳定控制时，通常采用对数转换方法对安全避撞不等式约束条件进行转换，这种方法的速率较低，因此系统达到稳定的速率相对较慢，无法满足特定场景对高速率响应特性的需求。此外，传统控制方法中对系统不确定性考虑较少，因而也存在控制精度不足的缺陷。对此，本实施例提出一种具有更快收敛速度及更小误差的分段函数状态转换方法和一类考虑时变不确定性的自适应鲁棒控制方法。该方案能在不确定性扰动存在的情况下满足agv队列系统运动过程中单个成员及整体系统的全局避撞性以及实现agv队列稳定性控制。
[0075]
具体地，如图1所示，本实施例提供的一种基于高速状态转换模型的agv队列的避撞控制方法包括如下步骤：
[0076]
s1：基于牛顿-欧拉方法构建agv队列系统的动力学模型。任意车辆i的动力学方程如下：
[0077][0078]
上式中，t表示时间，t∈r；χi表示车辆的位移；σi表示设计的不确定参数，ui表示控制力输入，ui∈r；mi表示第i辆车的质量；表示包括滚动阻力、加速阻力和其他外部干扰的行驶阻力的总和。在本实施例建立的agv队列的动力学模型中，函数mi(
·
)和fi(
·
)都是连续的，并且mi(
·
)是恒正的。
[0079]
s2：根据任意车辆与前车的实际车距si和理想车距的偏差建立误差函数ei(t)，并构建避撞约束。在初始安全条件下，任意车辆i与前车不发生碰撞的充要条件为：
[0080][0081]
上式中，表示第当前车辆i的前车的车身长度；si则表示第i辆agv与前一辆agv之间的实际车距。因此，在任何两辆相邻车辆不碰撞的情况下，状态si是单边界的(即si》0)。当实际车距si超过边界时，则说明碰撞可能发生。
[0082]
用代表第i辆agv与前一辆agv之间的理想车距，用ei来表示车距误差，则误差函数为：
[0083][0084]
此时，agv队列系统的避撞约束为：
[0085][0086]
s3：为了得到全局状态变量，本实施例进一步定义γ
i1
为一个与理想车距以及误差函数有关的第一状态参数，其对应的高速状态转换模型如下：
[0087][0088]
上式中的高速状态转换模型实际上是从单边有界状态到无界状态的一种映射，并有：与常用的对数状态转换函数相比，本实施例提出的高速状态转换模型能有效降低模型的求解难度，进而提升agv队列系统达到稳定状态收敛速率。
[0089]
s4：通过高速状态转换模型对误差函数进行转换，得到agv队列系统的车间距动力学方程。根据本实施例中的高速状态转换模型可以得到：
[0090][0091]
将上式关于时间t求导，可得：
[0092][0093]
整理得：
[0094][0095]
对上式再次求导，可得：
[0096][0097]
上式中，一阶系数和二阶系数分别为：
[0098][0099][0100]
定义γ
i2
为第二状态参数，且满足：则有：
[0101][0102]
根据动力学方程中任意车辆与前车不发生碰撞的充分必要条件，可得：
[0103][0104]
因此，给出转换后得车间距动力学方程如下：
[0105][0106]
其中，第三状态参数γ
i3
为：
[0107][0108]
s5：结合所述动力学模型以及车间距动力学方程中的状态参数，构建一个满足全局避撞约束的自适应控制器，包括如下步骤：
[0109]
s51：采用不确定系统分解方法，将agv队列系统的动力学模型中的参数分解为确定性部分和不确定性部分。agv队列系统的动力学模型的参数分解如下：
[0110][0111]
上式中，和分别表示第i个车辆的行驶阻力和质量的确定性部分；δmi和δfi分别表示第i个车辆的行驶阻力和质量的不确定性部分。假设函数δmi(
·
)，δfi(
·
)都是连续的，定义u-k方程中ψ(
·
)，δψ(
·
)，如下：
[0112][0113]
[0114][0115][0116]
则有，
[0117][0118]
s52：根据分解出的系统中的确定性部分，设置线性控制项u
i1
和反馈项u
i2
：
[0119][0120]
上式中，和分别表示第i个车辆的动力学模型中行驶阻力fi和质量mi的确定性部分；γ
i2
表示第二状态参数；和分别为第一状态参数的二阶导数中误差函数的一阶系数和二阶系数；γ
i3
表示第三状态参数。
[0121]
其中，
[0122][0123]
上式中，βi为一个自适应反馈控制系数，且满足：
[0124][0125]
s53：为了设计洗系统中的不确定性部分，提出如下假设：
[0126]
假设1：
[0127]
假设对于所有(χi，t)∈r
×
r，σi∈σi，存在已知函ρ
ei
(
·
):r
×r→
(-1，∞)使得
[0128]ei
(χi，σi，t)≥ρ
ei
(χi，t)
[0129]
假设2：
[0130]
假设对于所有存在未知常向量和一个个已知形式的未知函数πi(
·
):(0,∞)
sir×r×r×r→r
，使得：
[0131][0132]-δd
i-1
(u
i-1
f
i-1
)- δdi(u
i1
u
i2
fi)||
[0133]
≤πi(αi)
[0134]
函数一阶求导连续，是关于αi的凹函数；即：对于任意有：
[0135][0136]
为了估计不确定性参数αi的值，设计如下自适应律：
[0137][0138]
其中，参数用于估计参数αi；k1、k2均为大于0的常数。
[0139]
设置用于估计agv队列系统中的不确定性参数αi的自适应率，进而确定系统不确定性的补偿项u
i3
：
[0140][0141]
上式中，表示不确定性参数的估计值；表示不确定性参数的估计值；表示不确定参数αi的估计函数；表示函数的补偿函数；表示与有关的调整系数；γi表示求和函数项数。
[0142]
满足：
[0143][0144]
其中，
[0145][0146]
s54：设计包含线性控制项u
i1
、反馈项u
i2
和补偿项u i3
的自适应控制器；自适应控制器中的控制力输入ui为：
[0147]
ui＝u
i1
u
i2
u
i3
。
[0148]
s6：对采用自适应控制器的agv队列系统进行稳定性验证，并利用经过验证的自适应控制器实现agv队列系统的全局避障和稳定控制。
[0149]
定理1：
[0150]
取所提出的控制使得系统有如下性质：
[0151]
(1)一致有界性：对于任意ri≥0，存在di(ri)≤∞，若||δi(t0)||≤ri，则对于任意t≥t0，有||δi(t)||≤di(ri)。
[0152]
(2)一致最终有界性：对于任意ri≥0和当||δi(t0)||≤ri，存在di≥0使其中，t≥t0 ti(di,ri)，ti(di,ri)≤∞。
[0153]
如图2所示，一致有界性是指存在不确定性的系统在所有可能的初始情况下，系统状态方程的解总能处于某个有界范围内。一致最终有界性是指存在不确定性的系统经过一定时间，系统状态方程的解总能到达并限制在一个更小的范围区域。
[0154]
定理3：所提出的控制方法能确保系统只要开始时没有发生碰撞，则在行驶过程中避撞。
[0155]
定理4：在给定的控制式下，agv队列能保证系统的队列稳定性：对于任意ν≥0都存在一个ξ≥0使
[0156][0157]
使得对于所有t≥t0，均满足：
[0158]
sup||ei(t)||
∞
≤ν。
[0159]
实施例2
[0160]
在实施例1方案的基础上，本实施例还提供一种agv队列系统的避撞控制器，其采用如实施例1中的基于高速状态转换模型的agv队列的避撞控制方法中设计的自适应控制器；避撞控制器用于快速实现agv队列系统的队列成形和避撞控制。
[0161]
本实施例提供一种避撞控制器本质上是一种用于实现数据处理和指令生成的计算机设备，其包括存储器、处理器以及存储在存储器上并可在处理器上运行的计算机程序。处理器执行计算机程序时，创建出所需的集群控制器。
[0162]
本实施例中提供的计算机设备可以是能执行程序的智能终端、平板电脑、笔记本电脑、台式计算机、机架式服务器、刀片式服务器、塔式服务器或机柜式服务器(包括独立的服务器，或者多个服务器所组成的服务器集群)等。本实施例的计算机设备至少包括但不限于：可通过系统总线相互通信连接的存储器、处理器。
[0163]
本实施例中，存储器(即可读存储介质)包括闪存、硬盘、多媒体卡、卡型存储器(例如，sd或dx存储器等)、随机访问存储器(ram)、静态随机访问存储器(sram)、只读存储器(rom)、电可擦除可编程只读存储器(eeprom)、可编程只读存储器(prom)、磁性存储器、磁盘、光盘等。在一些实施例中，存储器可以是计算机设备的内部存储单元，例如该计算机设备的硬盘或内存。在另一些实施例中，存储器也可以是计算机设备的外部存储设备，例如该计算机设备上配备的插接式硬盘，智能存储卡(smart media card，smc)，安全数字(secure digital，sd)卡，闪存卡(flash card)等。当然，存储器还可以既包括计算机设备的内部存储单元也包括其外部存储设备。本实施例中，存储器通常用于存储安装于计算机设备的操作系统和各类应用软件等。此外，存储器还可以用于暂时地存储已经输出或者将要输出的各类数据。
[0164]
处理器在一些实施例中可以是中央处理器(central processing unit，cpu)、图像处理器gpu(graphics processing unit)、控制器、微控制器、微处理器、或其他数据处理芯片。该处理器通常用于控制计算机设备的总体操作。本实施例中，处理器用于运行存储器中存储的程序代码或者处理数据。
[0165]
仿真实验
[0166]
为了验证本实施例提出的一种基于高速状态转换模型的agv队列的避撞控制方法的实际应用效果，本实验以一个三辆车组成的自动车辆队列系统为控制对象，利用本实施例方法对自动车辆队列系统的编队运动过程进行协同控制。
[0167]
在本实施例的车辆队列系统中，三个车辆的具体参数包括：
[0168]
车辆质量选择：不确定质量选择如下：δm0＝15sint，δm1＝20sin 2t，δm2＝10 sin 3t。阻力选择如下：不确定阻力选择如下：δf0＝5 sin 0.2t，δf1＝10 sin 0.4t，δf2＝15sin0.6t。期望车距车身长度li＝1.2。
[0169]
控制参数选择如下：γ1＝1，γ2＝1ε1＝1,ε2＝1。根据初始车距误差的不同，将示
例分为两种情况。第一个示例中，-s
i＊
≤ei≤0，初始条件选择下：x(0)＝[30 27.3 25]
t
，，在第二个示例中，ei≥0，初始条件选择如下：x(0)＝[30 25.521]
t
，，
[0170]
图3和图4显示了两种初始情况下三辆车的位置关系。从图中可以发现：在第一种情况下，车辆之间的初始车距大于理想值，在3秒左右达到理想车距。在第二种情况下，车辆之间的初始车距大于理想值，在3秒左右后均达到理想值。
[0171]
图5和图6描述了两种情况下三辆车的速度。从图中可以发现：在第一种情况下，第二辆车和第三辆车由于过于紧凑而迅速减速以缩短距离。第二种情况下的第二和第三辆车通过提高速度缩短了与前车的车距。两辆跟随车在几秒钟后达到了与领航车辆相同的速度。
[0172]
图7和图8显示了两种情况下系统理想车距和实际车距的误差的变化曲线。从图中可以发现：两种情况在5s内误差均可以从高峰逐渐降低到0，这验证了本实施例提出的控制方法的有效性。
[0173]
图9和图10显示了两种情况下车辆2和3的控制力输入z2和z3的变化，从图中可以看出：二者存在波动但表现出良好的跟随状态。
[0174]
图11-图14显示了不同情况和对象间，使用两个不同的变换函数对距离误差对比。从图中数据可以看出，采用本实施例提出的分段的高速状态转换模型时，相比对数转换函数无明显的超调和震荡现象，且误差稳定时误差波动较小。
[0175]
综上所述，本实施例提供的基于高速状态转换模型的agv队列的避撞控制方法，在初始安全条件下，所设计的控制可以保证系统在行驶过程中不发生碰撞，并且可以保持在所规定的理想车距左右，从而可保证队列系统的紧凑性。另外，在系统控制中，每个跟随车辆只需要获取前一辆车的位置和速度信息，而不需要其他车的信息既可以实现整体的队列保持。同时，本实施例提出提出的控制策略能够保证一致有界性和一致最终有界性。
[0176]
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。